51. N皇后

发表于 | 分类于 | 阅读次数：

链接：https://leetcode-cn.com/problems/n-queens/

题目描述

n 皇后问题研究的是如何将 n 个皇后放置在 n×n 的棋盘上，并且使皇后彼此之间不能相互攻击。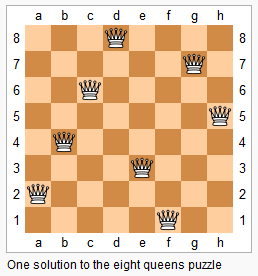
Alt text
上图为 8 皇后问题的一种解法。
给定一个整数 n，返回所有不同的 n 皇后问题的解决方案。
每一种解法包含一个明确的 n 皇后问题的棋子放置方案，该方案中 ‘Q’ 和 ‘.’ 分别代表了皇后和空位。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
示例:

输入: 4
输出: [
 [".Q..",  // 解法 1
  "...Q",
  "Q...",
  "..Q."],

 ["..Q.",  // 解法 2
  "Q...",
  "...Q",
  ".Q.."]
]
解释: 4 皇后问题存在两个不同的解法。

分析

N皇后问题是一个非常经典的深度搜索的问题。他的递归搜索树如下图所示：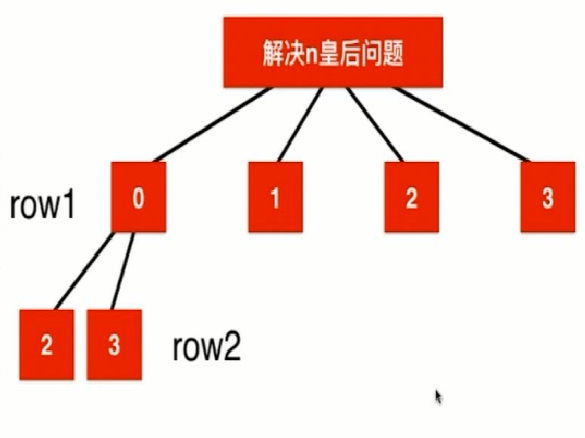
Alt text

它的最重要的一点就是我们如何快速的判断不合法的情况。
首先明确不合法的情况有：

  • 同一行不能有两个皇后：能在递归参数层面直接解决。
  • 同一列不能有两个皇后：使用一个标记数组标记当前列是否被占用。
  • 同一个对角线不能有两个皇后：
    • 对角线1：用一个标记数组表示第i对角线1被占用
    • 对角线2：用另一个标记数组表示第i对角线2被占用

这里最复杂的应该是对角线被占用的表示问题了，我们来看一下一种简便的表示方法：
对于对角线1如下图所示：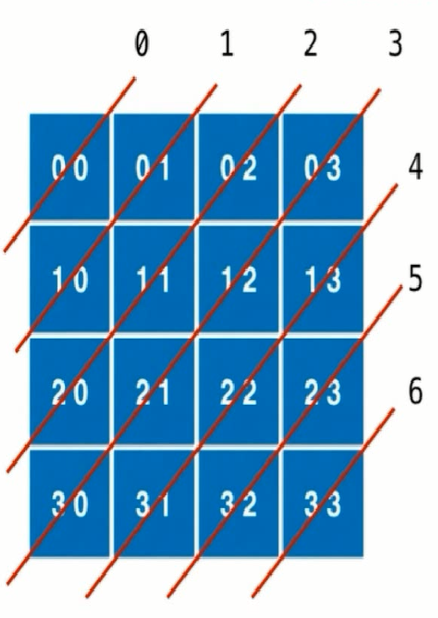
Alt text

它一共有2n-1个，并且每一条对角线i+j都是相等的。
对于对角线2如下图所示：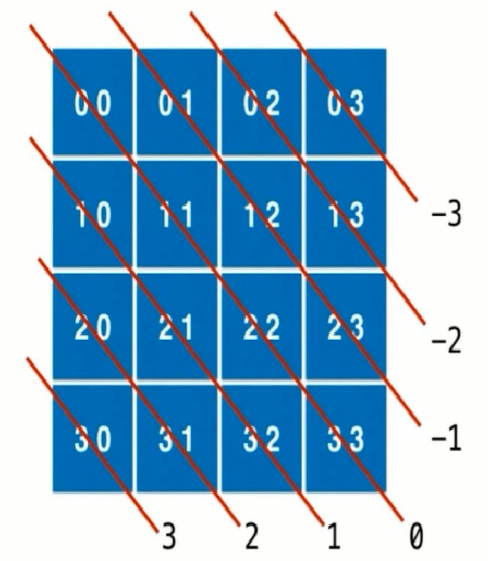
Alt text
同样也有2n-1个，它的规律是每一条对角线上两个元素相减是相等的，但是为了让它的结果能在0-2*n-1之间，所以我们使用i-j+n-1。
判断好了这几点，所以我们可以快速的写出答案了。

答案

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
class Solution:
    def __init__(self):
        # 列的标记数组
        self.cols = None
        # 对角线1的标记数组
        self.dia1 = None
        # 对角线2的标记数组
        self.dia2 = None
        # 最终结果
        self.result_all = None

    def solveNQueens(self, n: int):
        # 初始化一些数据
        self.cols = [0] * n
        self.dia1 = [0] * (2 * n - 1)
        self.dia2 = [0] * (2 * n - 1)
        self.result_all = []
        # 深度搜素
        self.dfs(n, 0, [])
        final_result = []
        for res in self.result_all:
            s = []
            for i, j in res:
                s_row = ["."] * n
                s_row[j] = 'Q'
                s.append("".join(s_row))
            final_result.append(s)
        return final_result

    def dfs(self, n, x, result):
        if x == n:
            self.result_all.append(result[:])
            return

        for y in range(n):
            if self.cols[y] == 1 or self.dia1[x + y] == 1 or self.dia2[x - y + n - 1] == 1:
                continue
            self.cols[y] = 1
            self.dia1[x + y] = 1
            self.dia2[x - y + n - 1] = 1
            result.append((x, y))
            self.dfs(n, x + 1, result)
            self.cols[y] = 0
            self.dia1[x + y] = 0
            self.dia2[x - y + n - 1] = 0
            result.pop()
        return